بحث عن دوال التغير ، كثير من الأشخاص والطلاب في مراحل التعليم المختلفة يجدون صعوبة في فهم دوال التغير الحسابية في مادة الرياضيات، ولذلك فإننا من خلال هذا المقال على موقع قلمي سوف نقوم بعمل بحث عن دوال التغير وتوضيح معناها بشكل مبسط مرفق بالأمثلة
بحث عن دوال التغير
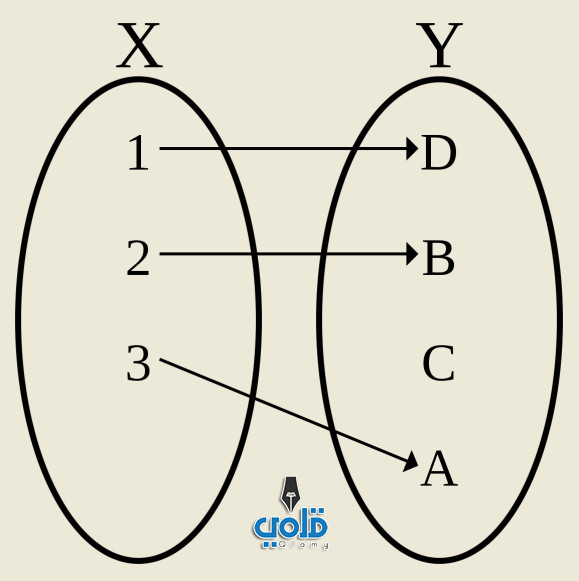
الدالة Function تعني وجود علاقة بين مجموعتين المجموعة الأولى هي المجال وكل عنصر فيها يمثله عنصر واحداً فقط في المجموعة الثانية وهي المجال المقابل أو المدى، ولا يمكن لعنصر من المجال أن يرتبط بأكثر من عنصر في المجال المقابل.
والمثال التالي يوضح معنى دالة التغير:
يوجد علاقة تناظر بين المجموعتين A وB
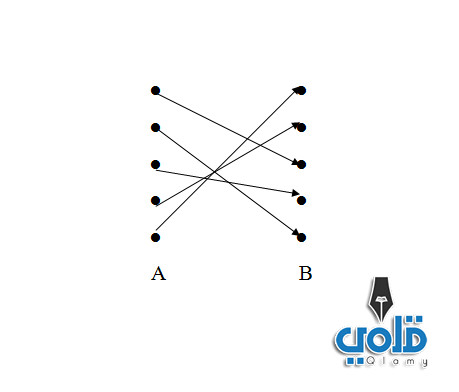
عناصر المجموعة A تسمى المصادر أو الأصول وتمثل مجال التناظر، وعناصر المجموعة B تمثل مدى التناظر والعناصر الذي يكون لها أصل في المجموعة A تسمى بالصور.
أشكال دوال التغير
دائما ما يتم استخدام الحروف الصغيرة للتعبير عن الدوال مثل حروف f, g أو س، ص
ويتم تمثيل الدوال بأكثر من شكل مثل:
التمثيل الجبري
التمثيل البياني
التمثيل بالقائمة
التمثيل بالكلام.
أولا: التمثيل للدالة بالطريقة الجبرية
المدى → المجال : f
د(س) = س2 + 3س + 5
مثال: معطاة الدالة د(س) = 3س + 1
أوجد صور المصادر التالية : 3، – 6، 2.5، 0، – 0.5
الحل:
د(3) = 3 (3) + 1 = 10
د(-6) = 3 (- 6) + 1 = – 17
د(2.5) = 3 (2.5) + 1 = 8.5
د(0) = 3 (0) + 1 = 1
د(- 0.5) = 3 (- 0.5) + 1 = – 0.5
ثانيا: التمثيل للدالة بالطريقة البيانية
في هذه الحالة يتم تمثيل عناصر المجال على محور س (X) وتمثيل عناصر المدى على محور ص (Y)، ويتم تمثيل كل عنصر وصورته في نقطة واحدة وبعد الحصول على عدة نقاط يتم ربط هذه النقاط ببعضها ويكون الشكل الناتج هو التمثيل البياني للدالة
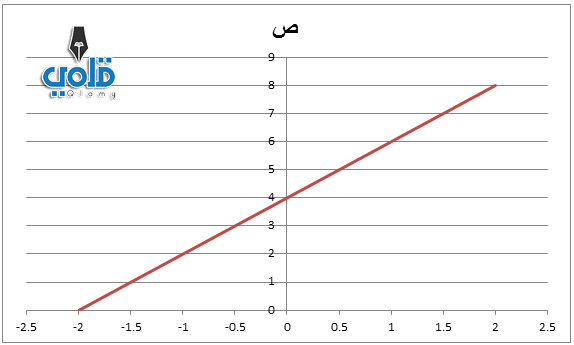
مثال: معطاة الدالة د(ص) = 2 س + 4
وقيم س هي: (2، 1، 0، -1، -2)
يتم الحصول على قيم ص من خلال التعويض بقيمة س
ص = 2 (2) + 4 = 8
ص = 2 (1) + 4 = 6
ص = 2 (0) + 4 = 4
ص = 2 (-1) + 4 = 2
ص = 2 (-2) + 4 = 0
|
س |
2 | 1 | 0 | -1 | -2 |
|
ص |
8 | 6 | 4 | 2 |
0 |
ثم يتم تمثيل نقطة التقاء كل عنصرين على إحداثيات س، ص كما هو موضح في الشكل التالي:
أنواع دوال التغير
يوجد أكثر من نوع من دوال التغير الحسابية ويتم تقسيمها كما يلي:
أولا: وفقا لعدد المتغيرات:
تنقسم دوال التغير من حيث عدد المتغيرات إلى دالة بمتغير واحد مستقل أو دالة لها 2 متغير مستقل أو دالة لها 3 متغيرات مستقلة.
ثانيا: وفقا للشكل الرياضي:
يوجد الدالة الثابتة وهي التي يكون مدى المجال بها مكون من رقم واحد فقط فتكون كل صور الأصول واحدة، ودالة التطابق وبها يكون كل عنصر في المجال له عنصر مطابق له في مدى المجال.
بالإضافة إلى الدوال الأسية واللوغاريتمية والجذرية والمثلثية.
 قلمي قلمي موسوعة قلمي الشاملة.
قلمي قلمي موسوعة قلمي الشاملة.